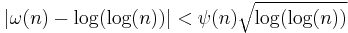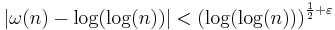Hardy–Ramanujan theorem
In mathematics, the Hardy–Ramanujan theorem, proved by Hardy & Ramanujan (1917), states that the normal order of the number ω(n) of distinct prime factors of a number n is log(log(n)). Roughly speaking, this means that most numbers have about this number of distinct prime factors. A more precise version states that for any real-valued function ψ(n) that tends to infinity as n tends to infinity
or more traditionally
for almost all (all but an infinitesimal proportion of) integers. That is, let g(x) be the number of positive integers n less than x for which the above inequality fails: then g(x)/x converges to zero as x goes to infinity.)
A simple proof to the result was given by Pál Turán.
The same results are true of Ω(n), the number of prime factors of n counted with multiplicity. This theorem is generalized by the Erdős–Kac theorem, which shows in fact that distinct prime factors are essentially normally distributed.
References
- Hardy, G. H.; Ramanujan, S. (1917), "The normal number of prime factors of a number", Quarterly Journal of Mathematics 48: 76–92, http://www.imsc.res.in/~rao/ramanujan/CamUnivCpapers/Cpaper35/page1.htm
- Hildebrand, A. (2001), "Hardy–Ramanujan theorem", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=H/h110080